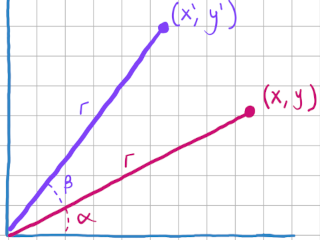
This is the first on what will be a series of posts showing the math behind commonly used formulas in graphics programming. In this post, we’ll take a vector (or a point) and rotate it by some amount about an origin. Take a look at the following diagram, rendered expertly below.

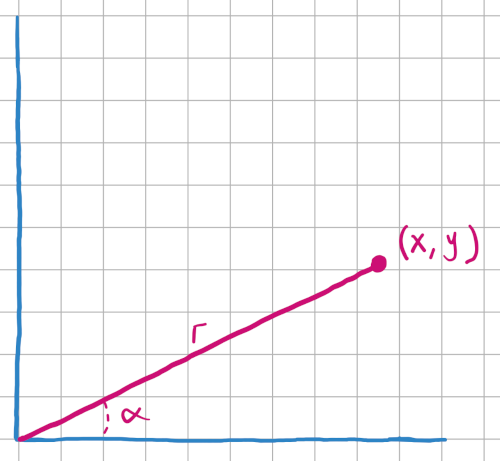
A figure showing a point at x, y at a rotation alpha

Here we have the original vector, before its been rotated. It sits at the coordinates (x, y). It has an angle alpha, and is a fixed distance r from the origin.

We can set up definitions for x and y based on the relationship between alpha and r.

$$ \begin{gather} cos \alpha = x / r \\ \Longrightarrow \\ x = cos \alpha * r \\ \rule{4cm}{1pt} \\ sin \alpha = y / r \\ \Longrightarrow \\ y = sin \alpha * r \end{gather} $$

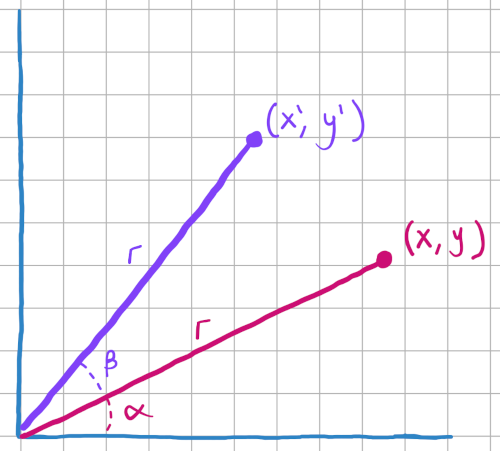
A figure showing two points, one at x, y with rotation alpha, the other at x' y' with rotation beta

Now say we rotate the original vector by beta degrees. It is still a distance of r from the origin, but it has a new x and y value. We’ll call these new values x’ and y'.

Let’s set up a definition of x’ and y’ based on the relationship between alpha, beta, and r. We’ll start with x':

$$ \begin{gather} cos (\alpha + \beta) = x’ / r \\ \Longrightarrow \\ x’ = cos (\alpha + \beta) * r \end{gather} $$

Thanks to the angle sum identities we know the following is true:

$$ cos (\alpha + \beta) = cos \alpha cos \beta - sin \alpha sin \beta $$

Let’s substitute out the equivalent identity and keep simplifying.

$$ \begin{gather} x’ = ( cos \alpha cos \beta - sin \alpha sin \beta ) * r \\ \Longrightarrow \\ x’ = cos \alpha cos \beta * r - sin \alpha sin \beta * r \end{gather} $$

Something about this equation seems familiar. Do you see nestled in the x’ definition our previous definitions of x and y? Let’s substitute those in!

$$ x’ = x cos \beta - y sin \beta $$

Stop here and try to get a definition of y’ in terms of x, y, and beta. You’ll need to use another angle sum identity. When you’re ready, here are the steps.

$$ \begin{gather} sin(\alpha + \beta) = y’ / r \\ \Longrightarrow \\ y’ = sin(\alpha + \beta) * r \\ \Longrightarrow \\ y’ = (cos \alpha sin \beta + sin \alpha cos \beta) * r \\ \Longrightarrow \\ y’ = r cos \alpha sin \beta * r + sin \alpha cos \beta * r \\ \Longrightarrow \\ y’ = x sin \beta + y cos \beta \end{gather} $$

You did it! For your convenience, here are the two final equations we derived today.

$$ \begin{gather} x' = x cos \beta - y sin \beta \\ y’ = x sin \beta + y cos \beta \end{gather} $$

The equations above could be represented by matrix multipication instead, if that suits your fancy.

$$ \begin{gather} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos \beta & -sin \beta \\ sin \beta & cos \beta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{gather} $$

So, why does the title of this post say, “about an origin?” You don’t have to use (0,0) as the point about which you rotate! Instead of calculating x’ and y’ from the x and y positions of the original vector, you can calculate it from the x offset and y offset of some arbitrary rotation point.

Say you have a vector of (5,5) you want to rotate around the point (3,3). Just use an x of 2 and a y of 2, as that’s the offset from the original point. I’ll leave the rest up as an exercise for the reader.

Next time I’ll write about how to project a 3D point to 2D, using perspective projection.