Using the Minimax Algorithm to Crack Tictactoe

Imagine you find yourself in a heated game of tic-tac-toe. Plotting your moves, you need to remember that each move you make should either get you closer to the win condition or move your opponent further from it. Of course, your opponent is going to be doing the same thing for each of their moves. While you can’t control how your opponent places their pieces to hinder you, each move has an effect on the options for the next player’s move. If you play your pieces right, you can limit your opponent’s ability to increase their advantage and decrease yours. To put it in more mathematical terms, with each move you’re looking to maximize your minimum possible advantage, and minimize your opponent’s maximum possible advantage.
This concept is key to a game theory algorithm called minimax. It can be applied elsewhere, but it’s very effective for optimally playing turn-based zero-sum games. A zero-sum game is one where the advantage of one player correlates directly to the disadvantage of another. The advantage and disadvantage cancel each other out, and you’re left with a sum of zero. Some examples of zero-sum games would be the aforementioned tic-tac-toe, checkers, chess, or Connect-4. Let’s dive deeper into the algorithm using tic-tac-toe.
As always, the code I’ve written is available on Github.
Generating a game state tree#
We can think of a game of tic-tac-toe as a tree. Each move is a branch on the tree. There are 9 options for the first move, 8 for the second, and so on. Our minimax algorithm will require such a tree.
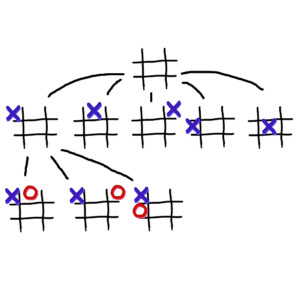
There are two ways to supply a minimax algorithm with a decision tree. We can either create the tree upfront, or generate the tree as we go inside the algorithm. Generating as we go allows us to only go through the game recursively a single time, otherwise we would need to do it twice: once for the tree generation and once again for the minimax algorithm.
Evaluating a game state for advantage#
The minimax algorithm will be traversing our tree, and evaluating the game state advantage of entries within the tree. We need some function where given a game state, we are returned some value representing advantage for either side. There’s no way to objectively quantify advantage, so this is the piece of minimax that’s a bit more of an art than a science.
For tic-tac-toe, what is our value function going to look like? This is what I came up with. We’ll be looking at the different ways in which a side can win the game, and how far along they are in each way. See the diagram below for an example, I’ll represent points with arrows.
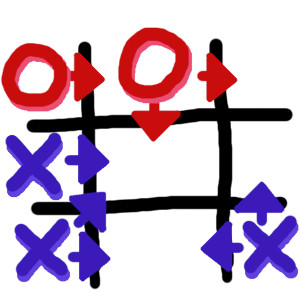
In the example above, Side-O can win along the top with only one more move (2 points). The middle column is also still possible (1 point), for a total of 3 points.
Side-X can win along the bottom row, with just one more move (2 points). They have access to a diagonal win as well (1 point). They get a point for having access to a middle row win (1 point), and a right column win (1 point). All this for a total of 5 points.
If a side has three in a row anywhere, their point value is now infinity. They’ve done it, they won. The final step to get the value is to subtract the opposing players value for the same position. This gets us a final value anywhere between negative and positive infinity. From Side-X’s point of view, this means the final value is 2.
Perceptive readers may have already noticed an apparent problem with the example above. Side-X is ahead by two points, despite the fact that Side-O is about to win with their next move! Our function doesn’t look to the future, only at what’s already on the board. It’s the minimax algorithm itself that’ll do the futuresight for us.
Minimaxing and the curse of futuresight#
With all that out of the way, we’re finally able to get to the meat and potatoes of the show. That’s a mixed metaphor, but here’s the good stuff. The minimax algorithm goes down our game state tree until it reaches a leaf (a node in a tree with no children) or it reaches its maximum depth. It then runs the value function I described above and has that value compared to all of that node’s siblings in the tree. The algorithm will select either the minimum value if it’s looking at an opposing player’s turn, or the maximum if it’s evaluating for the first player.
I was able to mostly follow the pseudocode for the algorithm that you can find on the minimax Wikipedia page. There are some minor tweaks I made, which I’ll discuss further below. In its entirety, here’s the minimax function I implemented, in Rust.
fn minimax<T: Copy + GameState>(state: &T, depth: i32, first_player: bool) -> (T, i32) {
let children = state.get_children(first_player);
if depth == 0 || children.len() == 0 {
let value = state.evaluate(true);
(state.clone(), value)
} else if first_player {
let mut maximum = i32::MIN;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, depth - 1, false);
if value > maximum {
maximum = value;
ret_state = child.clone();
}
}
(ret_state, maximum)
} else {
let mut minimum = i32::MAX;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, depth - 1, true);
if value < minimum {
minimum = value;
ret_state = child.clone();
}
}
(ret_state, minimum)
}
}
T is a generic type which implements the GameState interface. Here’s what that interface looks like.
pub trait GameState: Sized {
fn new() -> Self;
fn evaluate(&self, first_player: bool) -> i32;
fn get_children(&self, first_player: bool) -> Vec<Self>;
fn to_string(&self) -> String;
}
This way, I can write a solver for some other sum-zero game which implements the interface and this function should work without modifying this function.
Where the traditional pseudocode returns only the numeric value of the move it would make, my function returns a tuple of the game state of the suggested next move, as well as the numeric value. When the function is being called recursively, the numeric value is the only value used, but the original caller uses the returned game state to determine their next move.
Our minimax algorithm gets depressed#
Tic-tac-toe is a game in which it is trivial to force a tie. If you know the rules and you’re paying attention, there’s no real way you can lose. If you start in the center, and your opponent makes a mistake, you can put yourself in a situation where you win no matter what. Still, this strategy depends on your opponent fumbling, and they’re not likely to fall for the trick more than once.
Despite the trick not being foolproof, I hoped I would see the emergent behavior that the first move the algorithm picks is the center of the board. When I was setting the depth of the algorithm such that minimax’s futuresight could behold the entire game, I was disappointed to find it would pick instead the upper left corner for its starting play.
I spent close to two hours attempting to diagnose what was wrong with my implementation. It eventually dawned on me that nothing is actually wrong. With a far enough depth that minimax can see the entire game, it realizes that there’s no hope in playing to win and just picks the first space it sees, the upper left. The algorithm doesn’t account for human error, it’s assumed that the opponent player doesn’t put themselves in no-win situations if they can help it. So minimax has no way of figuring out that the middle space could lead to a potential win. Burdened with the curse of prophecy, minimax knows that a tie is the best it can hope for, and going for anything better would be fruitless. With too much lookahead, our minimax adopts nihilism.
Yet lowering the depth so minimax can only see five moves ahead has it placing its first move in the center, interestingly enough. If there’s a lesson here, maybe its to not worry so much about the future, and just do your best in the moment.
Optimizations#
While the algorithm works fairly fast for tic-tac-toe (consistently around 870 ms), other games are bound to be much more complicated. With added complexity would come a greater need for optimizations to improve performance. Let’s implement some of these optimizations and see how they impact our runtime.
Alpha-beta pruning#
The basic idea of alpha-beta pruning is to stop our evaluation once we reach a point where a child branch becomes incapable of influencing the values further upstream. When it becomes clear that a branch we’re going down is going to be poorer than another branch we’ve already looked at, we can take our gardening shears and lop of a significant percentage of the tree, which should improve our minimax’s performance.
fn minimax<T: Copy + GameState>(state: &T, depth: i32, mut alpha: i32, mut beta: i32, first_player: bool) -> (T, i32) {
let children = state.get_children(first_player);
if depth == 0 || children.len() == 0 {
let value = state.evaluate(true);
(state.clone(), value)
} else if first_player {
let mut maximum = i32::MIN;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, depth - 1, alpha, beta, false);
if value > maximum {
maximum = value;
ret_state = child.clone();
}
if value > beta {
break;
}
alpha = std::cmp::max(alpha, value);
}
(ret_state, maximum)
} else {
let mut minimum = i32::MAX;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, depth - 1, alpha, beta, true);
if value < minimum {
minimum = value;
ret_state = child.clone();
}
if value < alpha {
break;
}
beta = std::cmp::min(beta, value);
}
(ret_state, minimum)
}
}
By implementing pruning here, we get our minimax to finish consistently in about 490 ms. This is an improvement of 43%!
Adding a Transposition table#
The final optimization we’ll be looking at today is in adding a transposition table to our minimax function. Without it, the algorithm is doing a lot of repeat work. Say your first move is the upper left corner. Then, your opponent takes the center. Then, you take your second move in the upper right corner. This particular node in the game state tree is going to have six children, which are each going to have plenty of children of their own, and so on.
These children are going to be the exact same as for a different branch. Imagine your first move is the upper right. Then, after your opponent takes the center, you make your move in the upper left. What you have then is the exact same game state I described above, but a different sequence was taken to get there. We don’t need to evaluate the children of this branch, because it’s going to end up with the same result as the other.
If we add some sort of table which keeps track of the states the algorithm has already analyzed, we can prevent redoing any work we’ve already done. In implementation, a hash table does the job perfectly. We need to add a function to the GameState interface which can turn a game state into a string. The hashtable is going to take String keys and (T, i32) values. Any time our minimax function returns, we add to the transposition table. Before we do any evaluation of the tree, we check if the state already exists in the table, and we skip if it does. Here’s the function with the transposition table optimization added.
fn minimax<T: Copy + GameState>(
state: &T,
transposition_table: &mut HashMap<String, (T, i32)>,
depth: i32,
mut alpha: i32,
mut beta: i32,
first_player: bool,
) -> (T, i32) {
let children = state.get_children(first_player);
if depth == 0 || children.len() == 0 {
let value = state.evaluate(true);
transposition_table.insert(state.to_string(), (state.clone(), value));
(state.clone(), value)
} else if let Some(v) = transposition_table.get(&state.to_string()) {
*v
} else if first_player {
let mut maximum = i32::MIN;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, transposition_table, depth - 1, alpha, beta, false);
if value > maximum {
maximum = value;
ret_state = child.clone();
}
if value > beta {
break;
}
alpha = std::cmp::max(alpha, value);
}
transposition_table.insert(state.to_string(), (ret_state, maximum));
(ret_state, maximum)
} else {
let mut minimum = i32::MAX;
let mut ret_state = T::new();
for child in children.iter() {
let (_, value) = minimax(child, transposition_table, depth - 1, alpha, beta, true);
if value < minimum {
minimum = value;
ret_state = child.clone();
}
if value < alpha {
break;
}
beta = std::cmp::min(beta, value);
}
transposition_table.insert(state.to_string(), (ret_state, minimum));
(ret_state, minimum)
}
}
With a transposition table, the algorithm is completed in just 90 ms. This is an incredible improvement of 80% over the alpha-beta pruning only optimization, and a 90% decrease over no optimization at all.
Conclusion#
When it comes down to it, we don’t need these fancy game theory algorithms to write a tic-tac-toe AI. You could hack something together that operates without recursion, or any need for hash tables, or any use of a tree. But putting together a minimax algorithm to work for tic-tac-toe will give you the infrastructure you need to move onto vastly more complicated games, where more trivial solutions just aren’t possible. For the next game you’d like to solve with minimax, all you’ll really need is some way of numerically determining the value of a game state.
What’s next?#
As an exercise to the reader, I suggest implementing Connect-4 next. The value function is going to look very similar, since it too will involve looking along the board for connected pieces.